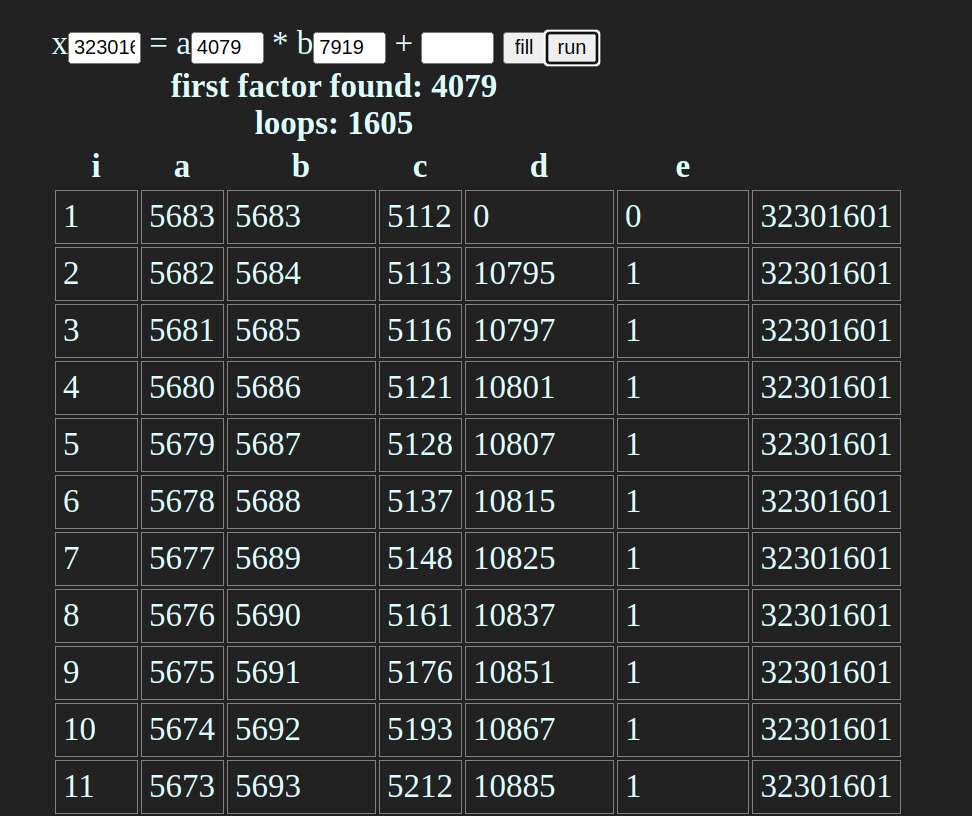
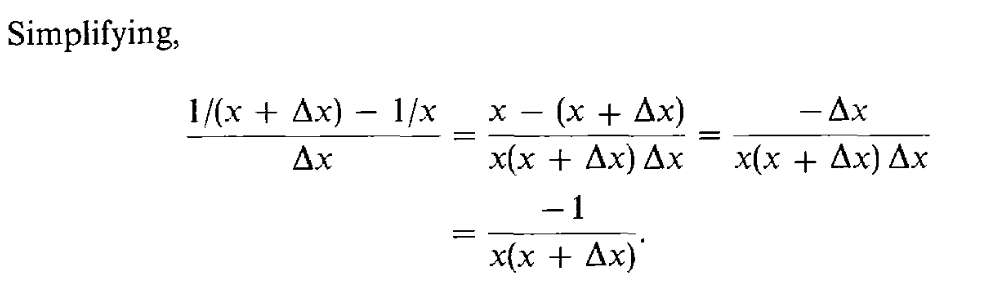So I started creating triangles in increasing size. For instance, I have three triangles T1, T2, and T3. T1 has 10 dots in it, T2 has 15, and T3 21.
10 15 21
.
. ..
. .. ...
.. ... ....
... .... .....
.... ..... ......
T1 T2 T3The more interesting part is that I could create squares by combining two consecutive triangles. For instance, combining T1 and T2 creates a square, and combining T2 and T3 also creates a square. By induction, this should hold for triangles of any size.
I wonder what other shapes I can create from rectangles.
Not sure how I could use this for factoring, but it's an interesting self-discovery. The question now is, given a square number, say, 196 = 14*14, how do I get the pair of two consecutive triangle numbers that add up to it. Well, aside from recursion.
Aha, wikipedia cheat to the rescue:
T1 + T2 = [(14**2)/2 + 14/2] + [(14**2)/2 - 14/2]
= 105 + 91
= 196I now have a roughly working algorithm for finding a factor given a number, and by extension, testing whether a given number is prime. It doesn't involve testing against a (possibly large) set of numbers. It's largely a conjecture if it holds for all numbers. I'm still working through examples that I think could be a counter-example, and thus prove the conjecture wrong. Since I'm not a mathematician, it's a long way for me to be able to formulate a mathematical proof. For now, finding counter-examples is easier.
The question is, will it be any better than the current algorithms? I don't know, depends on the complexity of finding the common factors between a number. I think gcd is pretty fast. Fast or not, it doesn't matter, it would be cool enough to create my own algorithm.
Well, it's midday of an early week in a yet another blazing hot day, and I'm lethargic as fuck again. There's lots of things I could do, or rather, I feel like I should do, yet here I am staring blankly at my untrimmed toe. I'm even too lazy to play games.
Maybe I should eat some chocolate. I had a long good sleep last night, yet I feel extra tired when I woke up.
Still, I should just do something, anything, however trivial or useless it is. Does typing all of this counts as doing something?
Actually I'm still working on my notebook, on my futile goal of trying to find other ways to factor a number. I do this before I start my day, while caffeine is still fresh in my biological systems. Why am still even working on it? Because I'm actually slowly making progress, I feel like I'm almost there. My gut feeling, could be wrong, is that there's no reason to resort to brute force when doing primality testing. What so special about prime numbers anyway?
Mathematicians defined a restriction that the factors should be natural numbers, but without that restriction, prime numbers are nothing special. I could also also try changing the unit other than 1. Yes, in my hypothetical universe where people have digit fingers of 1+N~, some (all?) primes become composite, and composite becomes prime.
But that's cheating, a math nerd would say. Yeah, but if my delusions turned out to be true, then prime numbers are mere superficial constraints imposed by our current mathematical system.
I have several algorithms that (at least appears to) work reliably well on small numbers. I could write programs to handle bigger numbers. It remains to be seen whether I could find (or prove) a general solution that works on any number. Or not, I'm just a lowly outsider to the art of mathematics. As always, I'm most likely just wasting my worthless time. No matter, my curiosity is fixated on doing this, I will keep on doing it, until I find something else to do.
No, find a job you stupid hiki-NEET.
Despite what non-binding nonsense I said yesterday, I'm still stuck on my notebook, slowly chipping away more dirt and mud. Maybe the fun hasn't worn off yet, or maybe I'm just too lazy to do anything else. Mucking around seems quite easy in comparison.
In any case, I should write down something. Not sure where to start, I should list down the seemingly useful formulas and equations that I found or made:
Firstly, I can decrement/increment any factors with any number
For any number n:
xy = (x+n)y - ny
xy = (x-n)y + ny
3(5) = (3+7)5 - 7(5)Another is this one:
x + y + ... = a(xa~ + ya~ + ...)
= a~(xa + ya + ...)Another one is this:
xy~ = 1 + (x-y)y~Also this:
ax + by + cz + ...
= (a + b + c + ...)(x + y + z + ...) - qRelated to this is the following observation (but not yet proven): For (my favorite) example, I have
469 = 7(67)
= 4(10^2) + 6(10) + 9
= 2(2*5)^2 + 2*3(2*5) + 3*3
^--a ^--b ^--cIs it useful? Initially, it thought it could be, but then, the search space is still quite large(r) when going for the brute force method of trying the all the different combination of factors.
So I'm trying the different angle, by looking for alternative or (even more) general ways of factoring, such as
ax + by + cz = (a + b + c)(x + y + z) - qI was going to write what I have been doing for the past 10 days but my mind got lost on fox digging holes. I mentioned Mr. Fox and digging holes because I thought it was an apt metaphor to what I've been doing.
Basically, I've scribbling a lot on my notebook, and it's pretty much what has been on my mind, even on my deep slumber. Unlike Mr. Fox, I wasn't running away from danger. I was just digging out of curiosity. Sure, they were infinitely better and meaningful things to do, but my mind was fixated on digging this hole. For my own detriment, it was almost the only thing I wanted to do for current time being.
My Digging was stupid and useless, and a complete waste of time. The only thing I would get out of this digging is to sink my life further. I was under no illusion that my digging would result into anything I would write home about (which is funny, because I'm always home). There's no glory here, it's all dirt, mud and worms.
Past the initial curiosity, digging turns into obsession, then suffering and borderline insanity. One night awoke in cold sweat three times to the same nightmare, believing I was almost there but there was nothing but a dead end.
In my mind, I was intoxicated with mad curiousity, thinking digging this part would reveal something, or would lead to something mankind has never ventured before. It was a dead end, but then I thought, what about this way, or that way. I could have consulted a pre-made map (by studying number theory), but no, I liked the feeling of ignorance and naivety, thinking there is more to what the eyes can see.
And this is where I am now. Thankfully, my manic episodes has died down a bit, and now I'm ready to go back and do some other projects. I'd say, I can't believe I've just wasted almost ten days digging for no purpose, but then it's completely plausible and in-character for me to do such a thing.
Of course, before I bury and cover up the hole, I should at least charter a map for the dungeons I've made. Which is to say, I should at least write down my own "self-discoveries", however trivial or unnew they are.
And my quest to devise my own manual long division continues. I tried dividing and factoring several numbers numbers in my notebook, some small and some large-ish. Several observations:
- if I can't get rid of the ~, then it's (likely) not evenly divisible
- I can express larger numbers as a sum of exponential 10s such as: 123 = 1*10^2 + 2*10^1 + 3*10^0
- I should avoid distributing ~ over the sum, since it becomes even harder to solve
- Sometimes I have to add terms together to make them factorable
-
I can further factor these base exponentials to help see some factors:
So here, I could see at a glance that 735 is evenly divisible by 5, without doing full division or factoring.735 = 7*10^2 + 3*10^1 + 5 = 7*5*2*5*2 + 3*5*2 + 5 = 5(7*2*5*2 + 3*2 + 1) - Going further, I could try converting base10 to another baseN to help see the factors at a glance (in theory, I haven't tried)
With that, my division method would then be first to factor out the divisor and the dividend (prime factorization it's called it seems), then cancel out any inverses. To some extent, it works. I managed to do division even for larger numbers like 12345.
Sadly, this doesn't necessarily mean that if I don't see any obvious factors then it's a prime number. Naively I thought that was the case, I quickly ran into counterexamples, most damning of which is the quadruply nice number 469, which is a product of two prime numbers 7 and 67!?! My supposed method broke down, all is lost, god is dead and/or mad, what am I even doing with my life again.
Just kidding (maybe). I'm just missing some important detail.
469
= (2^4)(5^2) + (2^2)(3)(5) + 3(3)
469
= 6(7)Then a thought occured to me: what are real numbers? Do they even exist? Aren't they just an artifact of decimal notation? Of course, some math teacher would bonk me in the head, and point to irrational numbers. But no, what if I want to reject the concept of real numbers, out of uncalled spite, and that irrational numbers can be perfectly expressed as a ratio of two numbers, with some slight tweak in the notation and the base axioms. Maybe these dumb irrationals belong on a separate number line.
Okay, if I'm asking these crazy questions, it's time to take a break. I'll probably answer and disprove my own questions sooner or later as I go along.
To continue from yesterday, to find a way to do factoring and division, I have to ask, what does division mean anyway? What does evenly divisible mean? What's remainder? With some faint recollection of some wikipedia article, after some scribbling, I manage to come up with:
x = ab + cMoving stuffs around:
x = ab + c (1)
x - ab = c (2)
xa~ = b + ca~ (3)
xa~ = b
65 = 2*x + c
Let x = 31
65 = 2*31 + c
65 = 62 + c
65 - 62 = c
c = 3What about if I let Let x = 32
65 = 2*32 + c
65 = 64 + c
c = 1What does this all mean for me? What does a negative remainder mean, and why don't I see it in the wild? Setting that aside for now, from here it's clear that 65 cannot be evenly be divided by 2 (where c = 0). But if I want to divide by 2 anyway, I get 32 with a remainder of 1.
Checking it in python:
>>> 65/2
32.5
xa~ = b + ca~ (3)
65*2~ = 32 + 1*2~
= 32 + 0.5
= 32.5
32.5 = 32 + 5*10~
= 32 + 1*2~Then again, I still don't have a methodical approach of doing long division besides doing trial and error. On the other hand, I could now do fizzbuzz without using the modulo operator. Well, actually I already did that before using a weird alien assembly language , but still.
Well, for some reason, now I'm trying to come up with my own division algorithm using only addition and multiplication. Partially, because I actually forgot how to do division by hand on paper, but also because of my curiosity to discover things for myself from first principles. Nothing new with what I'm doing, I'm sure someone already thought of these things around a thousand years ago.
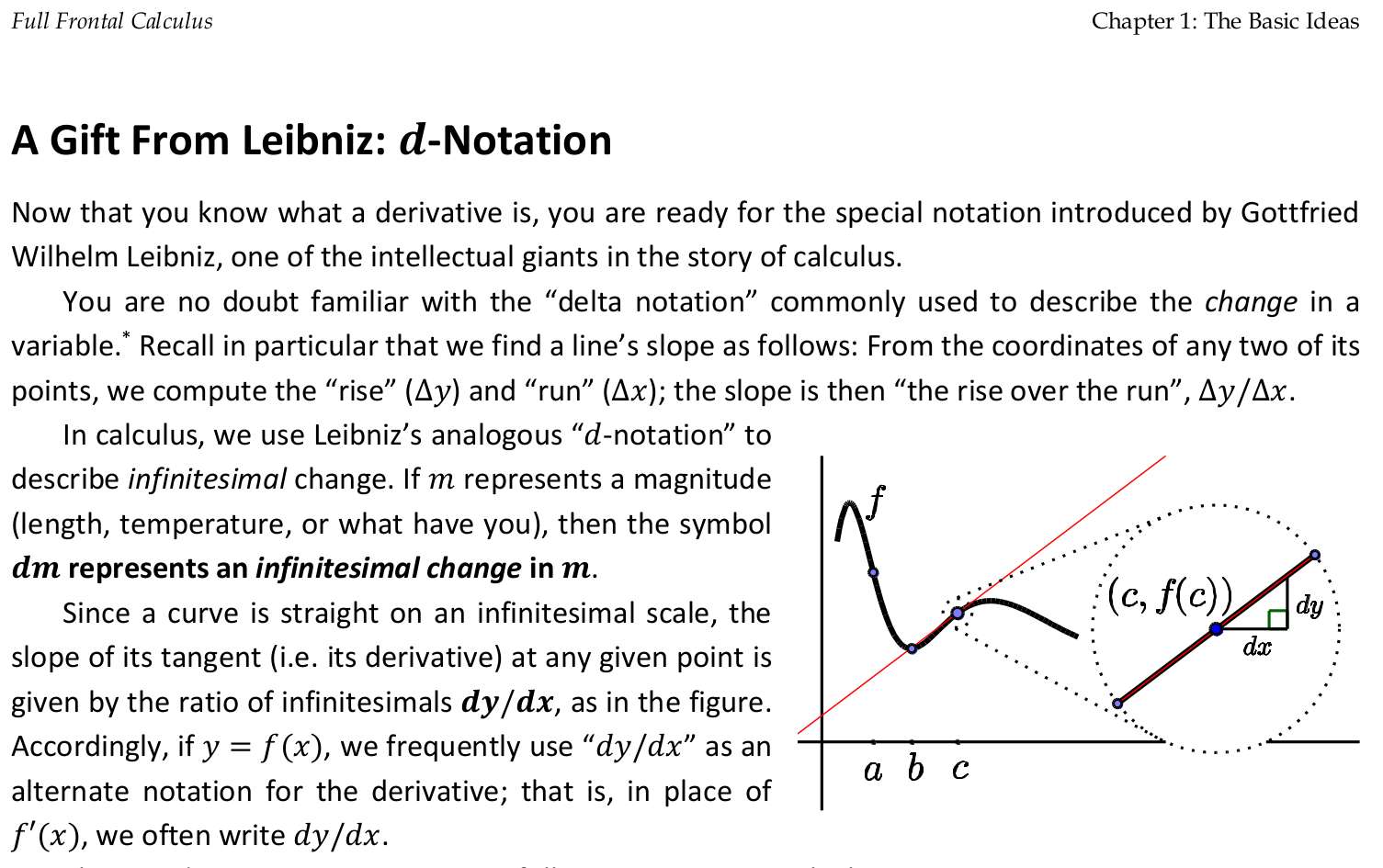
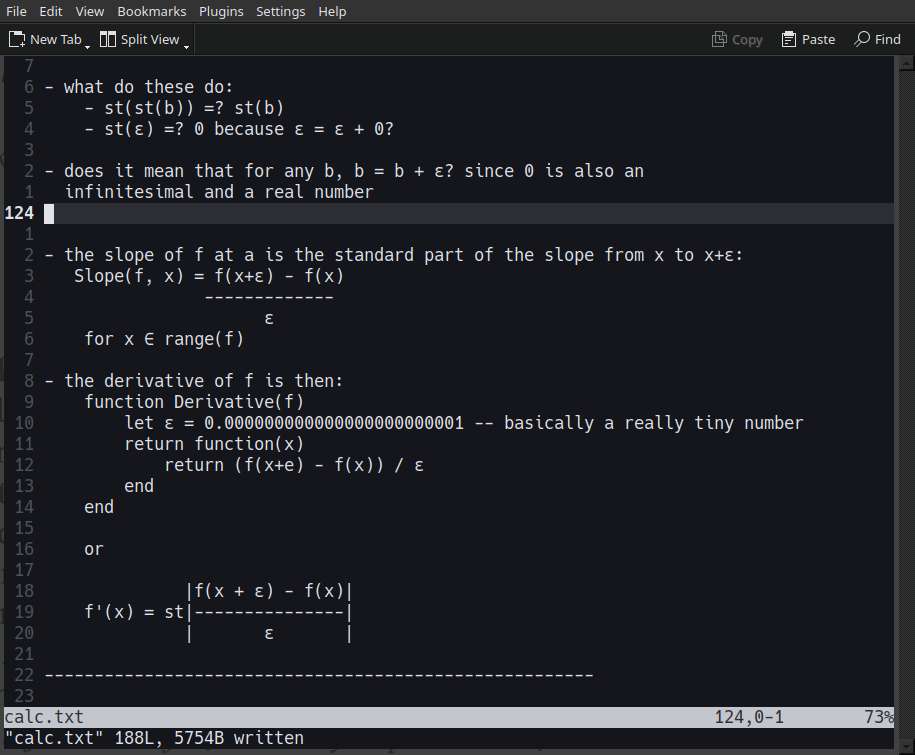
Continued reading FFC, or tried to read. On page 20, I see some very inadequate explanation for finding the derivative for x², at least compared to Keisler's explanation. It's probably more simpler, but now I have more question than answers if this was my first calculus book.
Well, to be fair, I'm not even reading intently that much, but at this point, I'm just looking for something to complain about. I'd be better off reviewing the earlier chapters of Keisler's book again.
Read a bit of Full Frontal Calculus (FFC), I mostly read and didn't do the exercises. I would have probably been already lost by page 15, but good thing I already have a good intuition of what this all means, so it's easier to follow. Basically, a recap.
Played around with my rocketbook again. I tried answering my own question, how do I express multiplication and division with addition and subtraction.
Multiplication of two numbers x and y is just
xy = x + x + x ... + x
^ y times
xy = y + y + y ... + y
^ x times
x + y = xy(x~ + y~)
xy = (x + y)(x~ + y~)~
xy = (x + y) / (x~ + y~)The sum of inverses sure do come up a lot, maybe there is another way of expressing it? What about
1 = 2~ + 2~
1 = 3~ + 3~ + 3~
1 = 4~ + 4~ + 4~ + 4~
1 = 5~ + 5~ + 5~ + 5~ + 5~
x + y = xy(x~ + y~)
xy(x~ + y~) = x + y
x~ + y~ = (x + y)x~y~
2~ + 2~ = (2 + 2)(2*2)~
2~ + 2~ = 4(4)~
3~ + 3~ + 3~
= (3+3)(3~)(3~) + 3~
= (3+3)[(3)(3)]~ + 3~
= [(3+3)~(3)(3)]~ + 3~
= (_ + 3)[(_)*3]~
= ([(3+3)~(3)(3)] + 3)[[(3+3)~(3)(3)]*3]~What about expressing division in terms of addition or subtraction?
12 / 4
= 12 + -3 + -3 + -3
= 12 + -(3 + 3 + 3 + 3) + 3
= 12 + 3*4 - 3
12(4~) = 3
12(4~) = 3To fill my gaps in my intuition and understanding, I started reading another book called "Full frontal calculus" by Seth Braver. It's surprisingly amusing to read, particularly the writing style of the author, where he uses religiuous analogies to describe the divide between limit-based calculus and infinitesimal calculus. It's certainly a refreshing way of explaining as opposed to the a bit overly dry prose from the other calculus book I was reading. I don't suppose to say that this is better pedagogically speaking, but it's certainly more entertaining.
Played around with the notebook, I could more or less get apply the division rule with power rule and product rule. Or really, I only ever need sum rule and product rule. But I can see why there are separate rules for each, since it's not always trivial or obvious, even a bit tedious, to get the directive directly from just the sum and product rule.
But, I'm still not comfortable with the syntax. When it says differential of a dependent variable, it's talking about differential of a function, right? Then, it goes around adding functions together, which is essentially a type error. Likely, it's implied and goes without saying that it's the result of the function that's being added together, not the function themselves.
Nope, my entire being rejects this convention. Where's the fully typed math syntax, I want it.
So the book did actually and directly used product and power rule for the quotient rule. The approach I did was to start with y = uv~ and get the derivative. But then I wondered, what variable is ∆u and ∆v dependent on? The book used the following notation:
| y = uv | y + ∆y = (u + ∆u)(v + ∆v)
If I let u = w~, how would that affect ∆u? Will it be ∆u~?
Once again, I see and hated the implicit handwavy notations that mathematicians use. I tried explicity converting dependent variables to functions, but then I didn't do any better, it's actually more verbose:
let Y(x) = U(x)V(x)
let ∆Y(x, ∆x) = U(x + ∆x)V(x + ∆x) - U(x)V(x)
= [U(x) + U(∆x)][V(x) + V(∆x)] - U(x)V(x)
= (u + ∆u)(v + ∆v) - uv
where
u = U(x)
v = V(x)
∆u = U(∆x)
∆v = V(∆x)
let Y(x) = U(x)V(x)~
let ∆Y(x) = (u + ∆u)(v~ + ∆v~) - uv~Well, it's supposed to be covered by power rule and the product rule, but I'll check tomorrow. Anyways, I found stuffs on HN that could also fun to learn: geometric algebra.
This tutorial seems to be readable for me https://mattferraro.dev/posts/geometric-algebra only highschool algebra is required.
I'm getting too distracted again though, the last thing I want to surfacely jump from one subject to another without actually ever learning anything. I wonder at what point I will stop reading the calculus book I'm reading right now. It's actually almost a thousand pages long. I could probably stop right until integral calculus, then maybe come to it later in the future.
I'm still reading the book "calculus: an infinitesimal approach". I'm on page 60, and briefly went over the rules for deriving rational functions. Nothing surprising so far, I can still follow along without problem. I should probably frequently go back to these pages and commit these rules into memory.
My eye twitched a bit on the quotient rule though. Isn't division just multiplication with inverses (a/b = ab^-1)? So there shouldn't be a special rule for this, it's covered by the power rule, right?
I'll check just to be sure.
Did some "studying" on my rocketbook with calculus notations. I tried writing it in a lua notation so it would be clear what scope each variable is, and are the dependent variables.
One thing I did realize is that Δx is not locally scoped inside the derivative, and that ε isn't really an independent variable as the book suggests.
So once I again, I will try to start from scratch, and write all the functions and equations:
let ∆x be any infinitesimal
let dx = ∆x
let f: func(x: *R)
let derivative = f => x => st{ [f(x + ∆x) - f(x)]∆x~ }
let differential = f => x => derivative(f)(x) * dx
let x be any infinitesimal
let y = f(x)
let slope = derivative(f)(x)
let dy = differential(f)(x)I found an HN post linking to a page of cool stuffs that applies math with programming. In particular, there's Differential equations and calculus from scratch which is highly relevant to what I'm doing.
I reviewed the notations for derivatives and differentials. I understand it now, but somehow I don't feel all too comfortable with it, maybe it's the concept or the notation. Perhaps I could think of an alternative notation for expressing differentials and derivatives, preferrably something close to a programming language syntax.
Next time I'll be reading the rules for differentiating rational terms. These rules are what are usually taught in schools to be rote memorized I think.
Aha, I think I understand now. ∆y/∆x ≈ f'(x) does actually makes sense. I had an imprecise definition of derivative in my head. More precisely, the derivative f'(x) is
f'(x) = st(∆y/∆x)
f'(x) - (∆y/∆x)
= st(∆y/∆x) - ∆y/∆x
= ε
∆y/∆x ≈ f'(x)
∆y/∆x - f'(x) = ε // by definition of infinitesimal
∆y/∆x = f'(x) + ε
∆y = f'(x)∆x + ε∆xI did consider and downloaded other books about infinitesimal calculus, but I didn't find any mention of the increment theorem. It would probably be better if I skim through at least one of them, to further solidify my understanding. In the end the wikipedia page was enough to clear up my understanding. Or maybe, a weekend break, consisting of turning my brain off.
I'll spend more time getting used to the notation shown on page 56, and I'll need to have a very intuitive understanding of increment theorem, because it seems important to gloss over.
Okay, I think I am infinitely close to understanding what the heck increment theorem is supposed to mean.
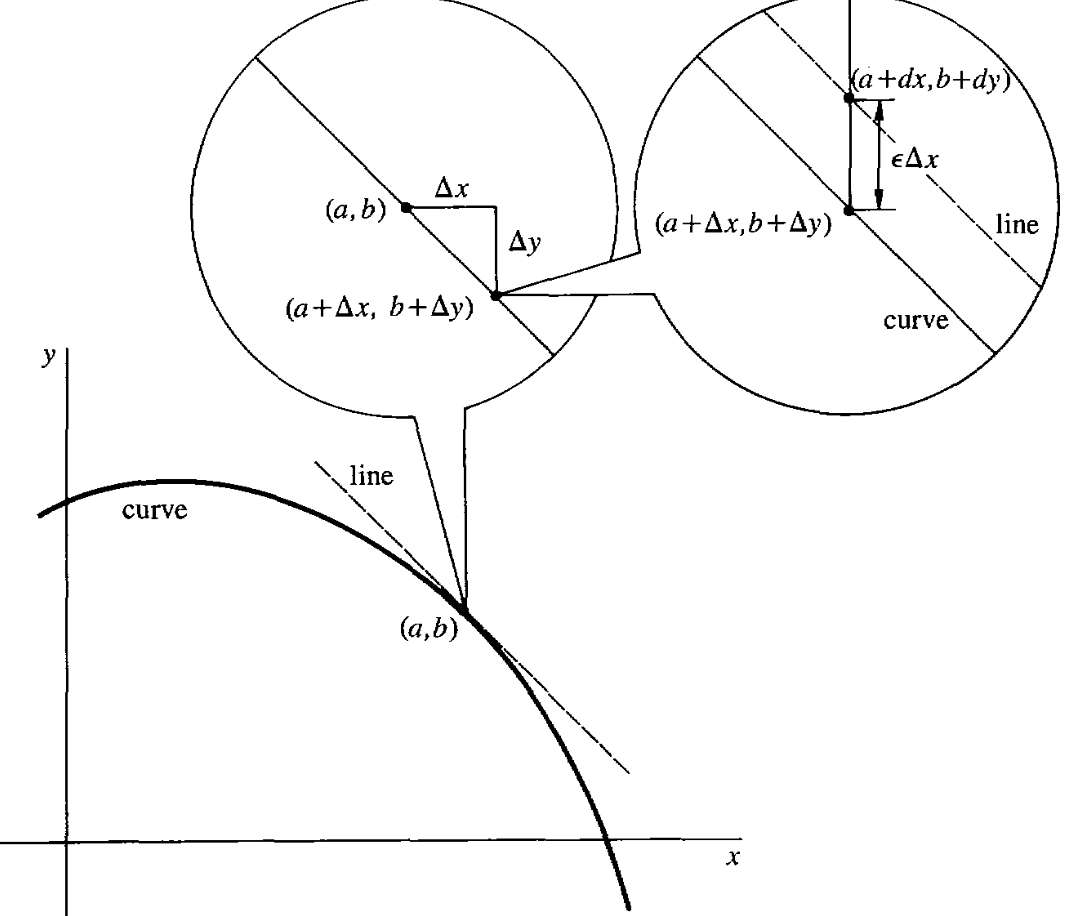
- I have a shitty curve f(x)
- derivative of f(x) is f'(x), which just maps x to a slope
- I can use the slope f'(x) to create a straight ass linear curve l(x)
Then at point [x, f(x)] and another point [x+∆x, f(x+∆x)] The change in y (f(x+∆x) - f(x)) along the f(x) is called "increment of y"?, notated as ∆y The change in y (l(x+∆x) - l(x)) along the l(x) is called "differential of y, notated as dy
The increment theorem says that the distance between ∆y and dy is εΔx, not that it helps why that matters.
Then somewhere in the book says that
∆y/∆x ≈ f'(x) (squiggly equal lines) and
dy/dx = f'(x)Well technically, any number x ≈ x since x-x = 0 + ε, so it could be that both ∆y/∆x ≈ f'(x) and ∆y/∆x = f'(x) is true.
Oh well, I may need to consult an alternative resource for a different explanation. At least for the increment theorem. I understood well what derivative and differential means. I should probably reviews the definitions for infinitesimal as well.
I wiped my most of my rocketbook pages, so I could have more space for weird symbols to scribble on.
Oh, I see I what's going on here:
l(x) - b = f'(a)(x - a)
l(x) = f'(a)(x - a) + bWhat I want:
- scoping of variable for each functions
- dependent variables should be clear whose variable it's depending on
- still have the freedom of doing algebraic manipulations (or equational reasoning? as the FP guys say)
lol, I didn't realize my computer crashed, all input was unresponsive, but it was still playing the same tune 3 second tune in a loop. Oddly enough, it still quite catchy, so I didn't notice until I tried moving my mouse.
Anyway, I was on my notebook wondering what the geometric interpretation of negative exponents. n^m makes sense, it just multiplication. But what about n^-m, it's not apparent at first, but it's just equal division. What about n^(m^-1)? n^0.5 is square root, but what does that mean? Isn't that division as well? Maybe unequal division?
As it turns out, I don't really understand the basic, fundamentals of math. But why stop at multiplication and division. Maybe there's a weird arithmetic operator that has useful properties. Base-2 has `xor`, `nand` and other operators.
What if xor and others was generalized to arbitrary base? So instead of bit-wise pairing, on decimal, it would be digit pairing. What properties woud those operator have?
Can I define some weird operators too? Programmers after all do that all the time, well, haskell programmers do at least.
I will set aside these thoughts for now, I have a calculus book to read.
I continued reading "calculus: an infinitesimal approach". I'm still following so far, but I don't quite get the increment theorem. For starters, why would ∆y be infinitesimal? If the book is referring to ∆y in the equation
∆y = f(x+∆x) - f(x)Of course, it's actually referring to a different(?) ∆y, the book is saying the ∆y in the equation
∆y = f'(x)∆x + ε∆xWhat I've learned just now:
- tagential line defined as l(x) - b = f'(a)(x - a) which is a line that intersects the point(a,b) with slope f'(a)
- change in y along the curve = f(x + ∆x) - f(x) change in y along the tangent line = f'(a)∆x
- differential of y and differential of x
- the change in y along the tangent line is called the differential of y, and is notated as dy, as opposed to ∆y, which is the changed in y along the curve
- dx and ∆x is the same, but dx is also used for notation consistency it seems
(x + y)~ = x~y~(x~ + y~)~
x + y = xy(x~ + y~)
x00~
(x^2)~ = x~2
x~^2 = x~2
x^(y~)
sqrt(x) = x^0.5 = x^2~
cbrt(x) = x^0.333.. = x^3~
(x^a)x~ = (x^a)(x^-1) = x^(a-1)
(x^a)^b = x^(ab)
(x^a)(x^b) = x^(a+b)
x^(n^-1)
x^(n^m) =? (x^n)^m
x^(2^3) =? (x^2)^3
x^8 =? (xx)^3
x^8 =? xx xx xxOh well, for today's morning, I've thought about why 0~ is undefined. Wikipedia gives me a lot of answers, but for some reason it still doesn't sit right with me. I should continue on with the calculus book, anyway, until I find another equation that seems difficult to solve with exponential notation.
I'll probably want to explore logarithms as well later.
= [(x+y)~ + -x~]y~
= [(x+y)~-x~(x+y + -x)]y~
= (x+y)~-x~yy~
= -(x+y)~x~Here's the list of theorems that I may find useful in my tedious journey of purely using exponential notations:
xy = (x~y~)~
x + y = x(1 + x~y) = y(1 + xy~)
x + y = xy(x~ + y~)
(x + y)~ = x~y~(x~ + y~)~
a(x+y)~ = [a~x+a~y]~I will set aside that thought, and I will continue forth. Uhh, why am I writing like this? I have a bloody headache right now, mostly because of I ran out of coffee, and caffeine withdrawal gives me a really bad headache.
Continuing from last friday, I found about multiplicative inverses conforming to de morgan's law:
xy~ = (x~y)~
x~y = (xy~)~
xy = (x~y~)~
[1/(x+y) - 1/x]/y
= [(x+y)~ - x~]y~
= (x+y)~y~ - x~y~
= [(x+y)y]~ - x~y~
= [xy+yy]~ - x~y~ // how do I go from this...
= ...
= -(x+y)~x~ // to this
(x+y)~ = ~x + ~y
(x+y)~ + -x~
= -y(x+y)~x~
= -(x+y)~x~y
(x+y)~ + x~
= (x+y)~yx~
-------------------------
= (x+y)~ + -x~
= (x+y)~xx~ + -x~(x+y)(x+y)~
= (x+y)~xx~ + -x~(x+y)(x+y)~
= [ xx~ + -x~(x+y) ](x+y)~
= [ x + -(x+y) ](x+y)~x~
= [ x + -x -y) ](x+y)~x~
= -y(x+y)~x~
x + y
= xyy~ + yxx~
= xy(y~ + x~)
x~ + y~
= x~yy~ + y~xx~
= x~(yy~ + y~x)
= x~y~(y + x)
x~ + y
= x~yy~ + yxx~
= yx~(y~ + x)
x + y~
= xyy~ + y~xx~
= y~x(y + x)
x~ + 0~
= x~0~(0 + x)
(x+y)~
= xy(x~ + y~)~
= [x~y~(x~ + y~)]~
= [(x~x~y~ + x~y~y~)]~
= [(x~2y~ + x~y~2)]~
= [(x~2 + x~2)y~]~
= (x~2 + x~2)~y
= (2x~2)~yLet me try again:
(x+y)
= xy(x~ + y~)
(x+y)~
= x~y~(x~ + y~)~
(x+y)~
= x~y~(x~ + y~)~
(x+y)~
= [ xy(x~ + y~) ]~
= [ xyx~ + xyy~ ]~
(x+y)~
= [xy(x~ + y~)]~
= xy(x~ + y~)]
1/(x+y) - 1/x
= (x+y)~ + -x~ // (A)
= (x+y)~xx~ + -x~(x+y)(x+y)~
= (x+y)~xx~ + -x~(x+y)(x+y)~ // common: x~,(x+y)~
= [ xx~ + -x~(x+y) ](x+y)~
= [ x + -(x+y) ](x+y)~x~
= [ x + -x -y) ](x+y)~x~
= -y(x+y)~x~
= -(x+y)~x~y // (B)Welp, this sucks, I feel like I'm going in circles. I should write and separate the equations that are shown to be true first.
I'm wondering now, why do I need to add the two fractions together before I could simplify it. Isn't there another way? That does sounds like a math trick that I must do without knowing why. That's what I tried before, but I couldn't get any further:
[1/(x+y) - 1/x]/y
= [(x+y)~ - x~]y~
= (x+y)~y~ - x~y~
= [(x+y)y]~ - x~y~
= [xy+yy]~ - x~y~ // how do I go from this...
...
= -(x+y)~x~ // to this
x~ + y~ = (x+y)x~y~
x~ + y~ = [(x+y)~x]~y~
x~ + y~ = [(x+y)~x]~y~ // TODO:
xy~ = (x~y)~ // ooh, this is actually true
x~y = (xy~)~ // woah, this holds as well
xy = (x~y~)~ // this too!?!?
xyz = (x~y~z~)~ // cool, it generalizes to arbitrary number of terms
// actually ~ behaves a like de morgan's law
x~ + y~
= (x + y)/(x*y)
x numerator
-----
y denominatorTo solve `1/x + 1/y`, I just need to make them have the same denominator:
1/x + 1/y
= (1/x)(y/y) + (1/y)(x/x)
= y/xy + x/xy
= (x+y)/xyNow I just need to translate this to exponential notation:
x~ + y~
= x~yy~ + y~xx~
= (yy~ + y~x)x~
= (x+y)x~y~----
Back to the previous problem, I need to simplify `(1/(x+y) - 1/x)/y`:
Simplify the numerator first
1/(x+y) - 1/x
= (x+y)~ + -x~ // (A)
= (x+y)~xx~ + -x~(x+y)(x+y)~
= (x+y)~xx~ + -x~(x+y)(x+y)~ // common: x~,(x+y)~
= [ xx~ + -x~(x+y) ](x+y)~
= [ x + -(x+y) ](x+y)~x~
= [ x + -x -y) ](x+y)~x~
= -y(x+y)~x~ // (B)
(1/(x+y) - 1/x)/y
= [ (x+y)~ + -x~ ]y~ // (A) times y~
= [ -y(x+y)~x~ ]y~ // replaced (A) with (B)
= -(x+y)~x~ // yy~ are inverses, so yy~ = 1
= -1/(x+y)*x----
I'm still not sure if avoiding fractional notation is better, but at least so far I've managed to avoid relying on special rules to do algebraic simplifications. I still don't know how the book was able to get `-1/(x+y)*x`, it just seems "magic" for me. Well actually, looking closer, the book did use the same trick by making both terms use the same denominator. It only just skipped lots of steps in between.
I skimmed over the book of abstract algebra last night, I didn't find anything I could use.
Played around more with equations, on paper, vim, and with python/sympy.
What I just realized is that, 1/(x+y) - 1/x can no longer be simplified. The book actually does simplification with (1/(x+y) - 1/x)/y
Second realization is that sympy does not automatically simplify when comparing equality between expressions. I seriously started questioning and doubting myself when it returns false with (a*b)*x == a*x + b*x.
I actually need to do simplify((a*b)*x) == simplify(a*x + b*x)
That said, the furthest simplification I got was
(1/(x+y) - 1/x)/y
= (x+y)^-1*(y^-1) + (-x^-1)*(y^-1)
(1/(x+y) - 1/x)/y
= (x+y)~y~ + -x~y~
(1/(x+y) - 1/x)/y
= (x+y)~y~ + -x~y~
= [(x+y)y]~ + (-xy)~
(1/(x+y) - 1/x)/y
= -1/(x*(x + y))
x~ + y~
= (x + y)/(x*y)
= (x + y)(x*y)~Ultimately, my goal is to show (to myself) that I can do algebraic manipulations without using fractions. It's a hill I'm willing to die on, probably. Or at least, lose a leg.
Aha, I found what I'm looking for:
(ab)^-1 = (a^-1)(b^-1)Now, I'm trying to follow an example of how to get the derivative of 1/x. Once again, whenever I see I fractions, I frequently scratch my head how did the book go from this to that. I should probably learn the basics how to combine fractions together, but I am weirdly fixed on notational purity, so I want to see could I solve this just in terms of exponents.
First, consider the equation:
1/(x+y) - 1/x
= 1/(x+y) + -1/x
= (x+y)^-1 + x^-1
(x+y)^-1 =? (x+y)1^-1
x^n = (x^a)(x^b) where n = a+bNope, it's even more complicated now, I've further strayed away from the light, the opposite of simplifying.
Oh well, I think I'll read the book of abstract algebra first.
I checked out sympy, a computer algebra system in python. sqrt(x)/x does indeed simplify to 1/sqrt(x). ... It took me too long to realize that sqrt(x) is not x^-2, but actually x^0.5
Nah, fuck this shit, I'm undoing all the changes I made today to moon-temple, I just added a bunch of pasta spaghetti monstrosity just to save me save keystrokes when reloading my changes.
On an unrelated note, I think I want to create a mini-simple computer algebra system, like an interactive math equation builder. That way, I'll have more fun manipulating equation with a keyboard. It'll be simple, just a symbolic modifier.
Something like this:
repl:
> expr = createExpression()
> expr // (nothing)
> expr.add(sym.x) // x
> expr.add(sym.x) // x + x
> expr.mul(sym.y) // (x + x)y
> expr.distribute() // xy + xy
> expr.factor(sym.x) // x(y + y)
> expr[1].combine() // x2y
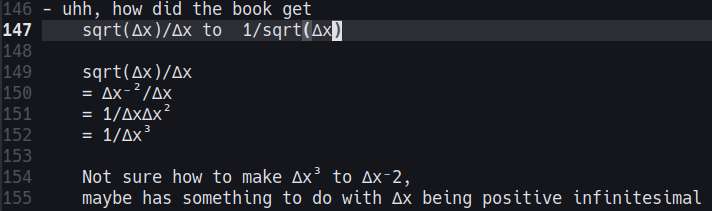
> expr.swap(1,2) // 2yxI continued reading the calculus book. I got stuck while following an example problem where sqrt(∆x)/∆x = 1/sqrt(∆x) and ∆x is a positive infinitesimal.
I can only get sqrt(∆x)/∆x = ∆x⁻²/∆x = 1/∆x∆x² = 1/∆x³ There's no way x³ = x⁻²
Oh well, maybe just a typographic error, or I'm just dumb. Not important anyway. Moving on.
I'm currently reading "Elementary calculus: An infinitesimal approach". I've been slowly reading for about an hour each day. But just a random thought, I should make a simple youtube web frontend, so that I could listen to longer videos while I sleep. I want the videos to stop playing automatically after 30 minutes, so it doesn't waste my phone batteries when I'm already deep slumber to listen.